学习《动手学习深度学习》的权重衰减这一节有些你内容做一下笔记,原文如下:
https://zh-v2.d2l.ai/chapter_multilayer-perceptrons/weight-decay.html
为什么要有正则化?
在训练参数化机器学习模型时,权重衰减 (通常称为L 2正则化)是最广泛使用的正则化的技术之一。这项技术是基于一个基本直觉,即在所有函数f 中,函数f =0(所有输入都得到值0)在某种意义上是最简单的,我们可以通过函数与零的距离来衡量函数的复杂度。
一种简单的方法是通过线性函数f ( x ) = w ⊤ x f(x)=w^⊤x f ( x ) = w ⊤ x ∥ w ∥ 2 ∥w∥^2 ∥ w ∥ 2 最小化训练标签上的预测损失,调整为最小化预测损失和惩罚项之和 。
果我们的权重向量增长的太大,我们的学习算法可能会更集中于最小化权重范数∥ w ∥ 2 ∥w∥^2 ∥ w ∥ 2
其实仔细想一下还是容易理解的,为了防止权重增量过大,我们将权重本身加入损失中进行迭代,如果权重大,那么损失值就大,就可以提升优化效果。
我们常用的处理过拟合的方法除了正则化 (权重衰减 )之外,还有:
增加训练数据;
使用适当复杂度的模型;
调节学习率的大小等。
如何将正则化添加入损失?
在线性回归中,我们的损失函数可以定义如下:
L ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 L(\mathbf{w}, b)=\frac{1}{n} \sum_{i=1}^{n} \frac{1}{2}\left(\mathbf{w}^{\top} \mathbf{x}^{(i)}+b-y^{(i)}\right)^{2}
L ( w , b ) = n 1 i = 1 ∑ n 2 1 ( w ⊤ x ( i ) + b − y ( i ) ) 2
为了惩罚权重向量的大小,我们需要以某种方式在损失函数中添加∥ w ∥ 2 ∥w∥^2 ∥ w ∥ 2 λ \lambda λ
L ( w , b ) + λ 2 ∥ w ∥ 2 L(\mathbf{w}, b)+\frac{\lambda}{2}\|\mathbf{w}\|^{2}
L ( w , b ) + 2 λ ∥ w ∥ 2
对于λ > 0 \lambda > 0 λ > 0 λ > 0 \lambda>0 λ > 0 ∥ w ∥ ∥w∥ ∥ w ∥
为什么除以2?
当我们取一个二次函数的导数的时候,就可以将前面的参数抵消,确保表达式简单。
为什么使用平方范数而不是标准范数(欧几里得距离)?
为了便于计算。通过平方L 2 L_2 L 2
为什么首先使用L 2 L_2 L 2 L 1 L_1 L 1
L 2 L_2 L 2 岭回归 (ridge regression)算法,L 1 L_1 L 1 套索回归 (lasso regression)。
使用L 2 L_2 L 2 L 1 L_1 L 1 特征选择 (feature selection),这可能是其他场景下需要的。
带L 2 L_2 L 2
w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) \mathbf{w} \leftarrow(1-\eta \lambda) \mathbf{w}-\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)}\left(\mathbf{w}^{\top} \mathbf{x}^{(i)}+b-y^{(i)}\right)
w ← ( 1 − η λ ) w − ∣ B ∣ η i ∈ B ∑ x ( i ) ( w ⊤ x ( i ) + b − y ( i ) )
我们根据估计值与观测值之间的差异来更新w w w w w w 权重衰减 衰减 权重。与特征选择(L 1 L_1 L 1 λ 值对应较少约束的w w w λ \lambda λ w w w
是否对相应的偏置b 2 b^2 b 2
代码实现
从零实现
我们根据下面这个公式来生成数据:
y = 0.05 + ∑ i = 1 d 0.01 x i + ϵ where ϵ ∼ N ( 0 , 0.0 1 2 ) y=0.05+\sum_{i=1}^{d} 0.01 x_{i}+\epsilon \text { where } \epsilon \sim \mathcal{N}\left(0,0.01^{2}\right)
y = 0 . 0 5 + i = 1 ∑ d 0 . 0 1 x i + ϵ where ϵ ∼ N ( 0 , 0 . 0 1 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 n_train, n_test, num_inputs, batch_size = 20 , 100 , 200 , 5 true_w, true_b = torch.ones((num_inputs, 1 )) * 0.01 , 0.05 train_data = d2l.synthetic_data(true_w, true_b, n_train) train_iter = d2l.load_array(train_data, batch_size) test_data = d2l.synthetic_data(true_w, true_b, n_test) test_iter = d2l.load_array(test_data, batch_size, is_train=False ) def init_params (): w = torch.normal(0 , 1 , size=(num_inputs, 1 ), requires_grad=True ) b = torch.zeros(1 , requires_grad=True ) return [w, b] def l2 (w ): return torch.sum (w.pow (2 )) / 2 def train (lambd ): w, b = init_params() net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss num_epochs, lr = 100 , 0.003 animator = d2l.Animator(xlabel='epochs' , ylabel='loss' , yscale='log' , xlim=[5 , num_epochs], legend=['train' , 'test' ]) for epoch in range (num_epochs): for X, y in train_iter: with torch.enable_grad(): l = loss(net(X), y) + l2(w) l.sum ().backward() d2l.sgd([w, b], lr, batch_size) if (epoch + 1 ) % 5 == 0 : animator.add(epoch + 1 , (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net, test_iter, loss))) print ("w的L2范数是:" , torch.norm(w).item())
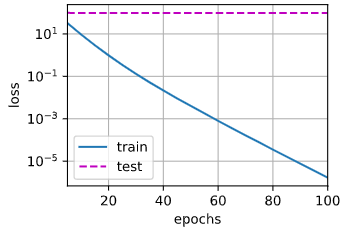
我们忽略惩罚项测试一下:
输出:w的L2范数是: 13.433332443237305.
设置惩罚项测试一下:
输出:w的L2范数是: 0.3840215802192688.
可以看见,没有L 2 L_2 L 2 L 2 L_2 L 2
使用深度学习框架实现
深度学习框架为了便于使用权重衰减,便将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处,允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次。
在实例化优化器时直接通过weight_decay指定weight decay超参数。默认情况下,PyTorch同时衰减权重和偏移。这里我们只为权重设置了weight_decay,所以bias参数b 不会衰减。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def train_concise (wd ): net = nn.Sequential(nn.Linear(num_inputs, 1 )) for param in net.parameters(): param.data.normal_() loss = nn.MSELoss() num_epochs, lr = 100 , 0.003 trainer = torch.optim.SGD([ {"params" :net[0 ].weight,'weight_decay' : wd}, {"params" :net[0 ].bias}], lr=lr) animator = d2l.Animator(xlabel='epochs' , ylabel='loss' , yscale='log' , xlim=[5 , num_epochs], legend=['train' , 'test' ]) for epoch in range (num_epochs): for X, y in train_iter: with torch.enable_grad(): trainer.zero_grad() l = loss(net(X), y) l.backward() trainer.step() if (epoch + 1 ) % 5 == 0 : animator.add(epoch + 1 , (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net, test_iter, loss))) print ('w的L2范数:' , net[0 ].weight.norm().item()) print (net)
正则化系数与train_acc、test_acc的关系
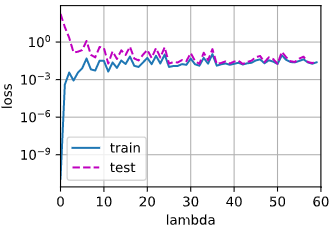
修改代码,取λ \lambda λ train_acc, test_acc, λ \lambda λ
一开始λ = 0 \lambda=0 λ = 0 λ \lambda λ λ > 4 \lambda>4 λ > 4
如果单单通过验证集来找最佳的λ \lambda λ λ \lambda λ λ \lambda λ
发现新正则
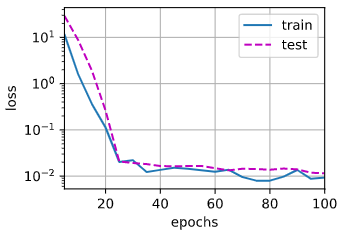
偶然的一次尝试发现这种正则的效果很好,所谓“很好”指的是训练损失和测试损失曲线在较少的epoch次之后就可以几乎重合。表达式如下:
L=\frac{1}{2}\sum e^{\abs{w}}
将正则换成新的正则函数之后,我们设置λ = 6 \lambda=6 λ = 6 train_loss和test_loss曲线:
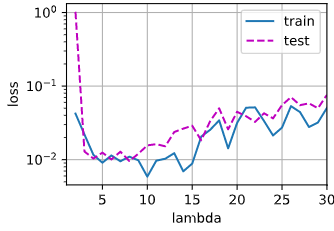
我们将代码改为不同的λ \lambda λ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 n_train, n_test, num_inputs, batch_size = 20 , 100 , 200 , 5 true_w, true_b = torch.ones((num_inputs, 1 )) * 0.01 , 0.05 train_data = d2l.synthetic_data(true_w, true_b, n_train) train_iter = d2l.load_array(train_data, batch_size) test_data = d2l.synthetic_data(true_w, true_b, n_test) test_iter = d2l.load_array(test_data, batch_size, is_train=False ) def init_params (): w = torch.normal(0 , 1 , size=(num_inputs, 1 ), requires_grad=True ) b = torch.zeros(1 , requires_grad=True ) return [w, b] def l2 (w ): return torch.sum (torch.exp(abs (w))) / 2 def train (lambd ): w, b = init_params() net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss num_epochs, lr = 100 , 0.003 for _ in range (num_epochs): for X, y in train_iter: with torch.enable_grad(): l = loss(net(X), y) + l2(w) * lambd l.sum ().backward() d2l.sgd([w, b], lr, batch_size) return (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net, test_iter, loss))
1 2 3 4 5 6 animator = d2l.Animator(xlabel='lambda' , ylabel='loss' , yscale='log' , xlim=[1 , 30 ], legend=['train' , 'test' ]) for i in range (1 , 30 ): train_loss, test_loss = train(lambd=i) animator.add(i + 1 , (train_loss, test_loss))
下图是取不同的λ \lambda λ λ \lambda λ