参考：

PyTorch Autograd Explained-In-depth Tutoral

使用pytorch的backward()报错

使用pytorch的backward函数的时候报错：RuntimeError: grad can be implicitly created only for scalar outputs。

观察下面这段代码：

import torch

x = torch.tensor(2.3, requires_grad=True)
y = 2 * x
y.backward()
print(x.grad)

输出结果为：2.0

x是一个标量，当调用它的backward方法后会根据链式法则自动计算出叶子节点的梯度值，如果将其换成一个矩阵或者向量呢？

import torch

x = torch.randn((3, 4), requires_grad=True)
y = 2 * x
y.backward()
print(x.grad)

得到报错：RuntimeError: grad can be implicitly created only for scalar outputs

如果 Tensor 是一个标量(即它包含一个元素的数据），则不需要为 backward() 指定任何参数，但是如果它有更多的元素，则需要指定一个 gradient 参数，该参数是形状匹配的张量。

那么为了解决上面代码的问题，需要将第5行改成如下：

1
2
3

y.backward(gradient=torch.ones_like(x))
# 或者改成：y.sum().backward()
# 使用sum的话得到的就是各元素之和，得到的就是一个标量，可以求梯度

输出结果如下：

1
2
3

tensor([[2., 2., 2., 2.],
        [2., 2., 2., 2.],
        [2., 2., 2., 2.]])

当然，最常用的是传入torch.ones_like(x)函数，也可以传入其他的张量给gradient参数，比如下面这段代码：

x = torch.tensor([2., 1.], requires_grad=True)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)

z = torch.mm(x.view(1, 2), y)
print(f"z:{z}")
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")

输出结果如下：

z:tensor([[5., 8.]], grad_fn=<MmBackward>)
x.grad: tensor([1., 3.])
y.grad: tensor([[2., 0.],
        [1., 0.]])

z容易理解，就是两个矩阵x和y相乘的结果，反向传播的时候，计算流程如下图所示：

源代码中backward的接口定义如下：

torch.autograd.backward(
		tensors, 
		grad_tensors=None, 
		retain_graph=None, 
		create_graph=False, 
		grad_variables=None)

grad_tensors的作用其实可以简单地理解成在求梯度时的权重，因为可能不同值的梯度对结果影响程度不同，所以pytorch弄了个这种接口，而没有固定为全是1。

PyTorch Basics

Tensors：张量在Pytorch中相当于一个高维数组，除了可以加载到CPU，张量还可以加载到GPU从而加速计算。只要将一个张量的参数设置为：requires_grad=True，他们就会自动构建反向传播计算图，并跟踪每一次在该张量上的运算，以便于使用静态计算图（dynamic computation graph）来计算张量。

在早期版本的pytorch中，torch.autograd.Variable类被用来创建支持梯度计算和操作符跟踪的张量，但是Torch v0.4.0中Variable类已经被弃用了。现在在pytorch中，torch.Tensor和torch.autograd.Variable是同一个类，而且前者更适合用于跟踪运算符。

一个权重参数的梯度可以理解为：该权重的一个微小改变导致的损失值的改变。随后该梯度被用于更新权重。

注意，在pytorch中，只有浮点型的张量才可以计算梯度。可以使用如下的方式快速转换：
1
2
3
4
5
6
7
8
9
10
11
import torch

x = torch.randint(1, 5, (2, 3))
print(f"Int type x: \n{x}\n")
x = x.type_as(torch.FloatTensor(x.shape))
x.requires_grad_(True)
print(f"Float type x: \n{x}\n")

y = x ** 2
y.backward(torch.ones_like(x))
print(f"x.grad: \n{x.grad}\n")

Autograd:这个类记录了在一个gradient enabled张量上的所有运算符，并创建了一个静态计算图。这个计算图中，输入结点表示叶子节点，输出结点是根节点。梯度的计算是通过从根节点走到叶子节点，使用链式法则，将沿途上所有的梯度相乘得到最终叶子节点的梯度。

静态计算图（Dynamic Computational graph)

静态计算图由gradient enabled 张量和操作符共同偶见。数据流与在该数据流上的运算符在运行时就定义了，所以静态计算图的构建完全是自动的。一个设置requires_grad=False的简单相加操作的计算图构建如下（图片来自https://towardsdatascience.com/pytorch-autograd-understanding-the-heart-of-pytorchs-magic-2686cd94ec95）：

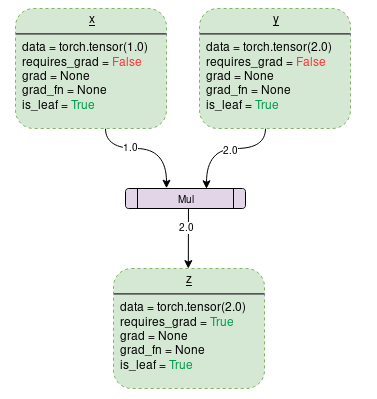
每一个虚线框表示的是图中的一个变量，紫色矩形框是一个操作符。

每一个变量都有如下的属性成员：

Data:变量的数值。

requires_grad:这个属性如果设置为True，就开始跟踪所有的操作符然后构建一个反向传播图用于计算梯度，对于任意一个张量，创建之后可以通过a.required_grad_(True)来改变其状态。

grad:这个属性表示变量的梯度值。如果requires_grad是False，那么grad值就是None，即便requires_grad是True，变量的grad属性也不能立马变成有值的状态，还需要根节点的.backward()函数操作之后才可以有梯度值。

grad_fn:该属性记录了用于计算梯度的反向传播函数。

is_leaf:如果一个节点满足以下条件之一就是叶子结点：

1. 该结点变量通过一些函数来显示初始化，比如`x=torch.tensor(1.0)`或者`x=torch.randn(1, 1)`。
2. 在对所有`requires_grad=False`的张量经过运算符操作之后创建的结点。
3. 它是通过一些张量的`.detach()`创建的。

一旦根节点执行了backward()，梯度只会被填充到requires_grad和is_leaf均为True的结点上。

如果设置requires_grad=True，pytorch会开始追踪操作符，并且将每一步的requires_grad=True的变量的梯度函数存储起来，就像下图一样（图来自https://towardsdatascience.com/pytorch-autograd-understanding-the-heart-of-pytorchs-magic-2686cd94ec95）：

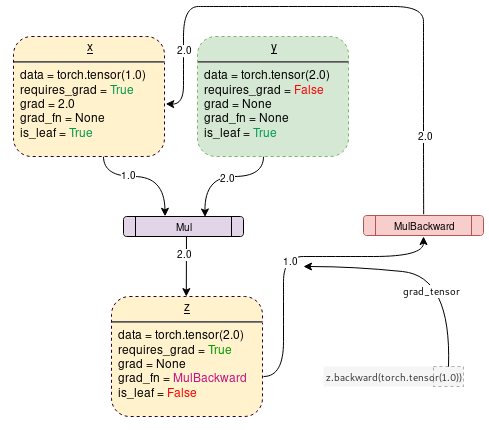
下面这段代码可以生成上述的计算图：

import torch

# Creating the graph
x = torch.tensor(1.0, requires_grad = True)
y = torch.tensor(2.0)
z = x * y

# Displaying
for i, name in zip([x, y, z], "xyz"):
    print(f"{name}\ndata: {i.data}\nrequires_grad: {i.requires_grad}\n\
grad: {i.grad}\ngrad_fn: {i.grad_fn}\nis_leaf: {i.is_leaf}\n")

如果要防止pytorch追踪运算与创建反向传播图，可以将代码片段包含在with torch.no_grad():里，这可以让代码运行的更快，而且节省内存。

import torch
# Creating the graph
x = torch.tensor(1.0, requires_grad = True)
# Check if tracking is enabled
print(x.requires_grad) #True
y = x * 2
print(y.requires_grad) #True

with torch.no_grad():
	# Check if tracking is enabled
	y = x * 2
	print(y.requires_grad) #False

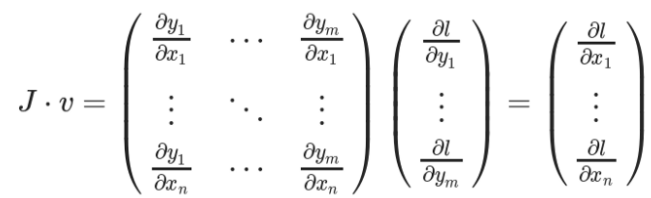
Jacobians and vectors

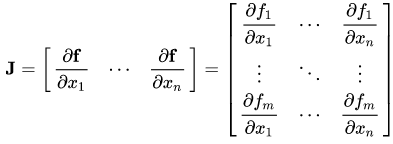
雅克比(Jacobians)矩阵：记录两个向量之间的偏导数关系。如一个向量 $X=[x_1,x_2...x_n]$ ，另一个向量 $f(x)=[f_1,f_2,...,f_n]$ ，那么雅克比矩阵 $J$ 表示如下：

假设一个pytorch的gradient enabled张量 $X=[x_1,x_2...x_n]$ （假设它表示的是一个机器学习模型中的权重），X经过一些操作之后得到 $Y=f(X)=[y_1, y_2, ...,y_m]$ 。

然后Y被用于计算标量损失 $l$ ，假设一个向量 $v$ 是标量损失 $l$ 相对于 $Y$ 的梯度向量：

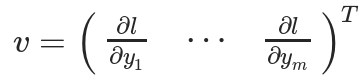
为了获得损失 $l$ 和权重 $X$ 之间的梯度，使用雅克比矩阵与 $v$ 相乘可以得到：

pytorch inplace operation

在pytorch中，有两种情况不能使用inplace operation：

对于requires_grad=True的叶子张量不能使用inplace operation；
对于在求梯度阶段需要用到的张量，不能使用Inplace operation。

第一种情况: requires_grad=True的leaf tensor

import torch

w = torch.FloatTensor(10) # w 是个 leaf tensor
w.requires_grad = True    # 将 requires_grad 设置为 True
w.normal_()               # 在执行这句话就会报错

报错信息为：

1	RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.

因为作为叶子结点，在设置requires_grad为True之后，计算图开始构建了，如果要在构建之后初始化权重可以这样：

import torch

w = torch.FloatTensor(10) # w 是个 leaf tensor
w.requires_grad = True    # 将 requires_grad 设置为 True
# w.normal_()      
w.data = torch.normal(0, 0.01, w.data.shape)

第二种情况：求梯度阶段需要用到的张量

import torch

x = torch.randint(1, 5, (2, 3))
x = x.type_as(torch.FloatTensor(x.shape))
print(f'x = \n{x}\n')

w = torch.randint(1, 5, (3, 2))
w = w.type_as(torch.FloatTensor(w.shape))
w.requires_grad_(True)
print(f'w = \n{w}\n')

d = torch.mm(x, w)
# x -= 1

d.sum().backward()
print(f'w.grad = \n{w.grad}')

将上述代码计算图构建出来如下：

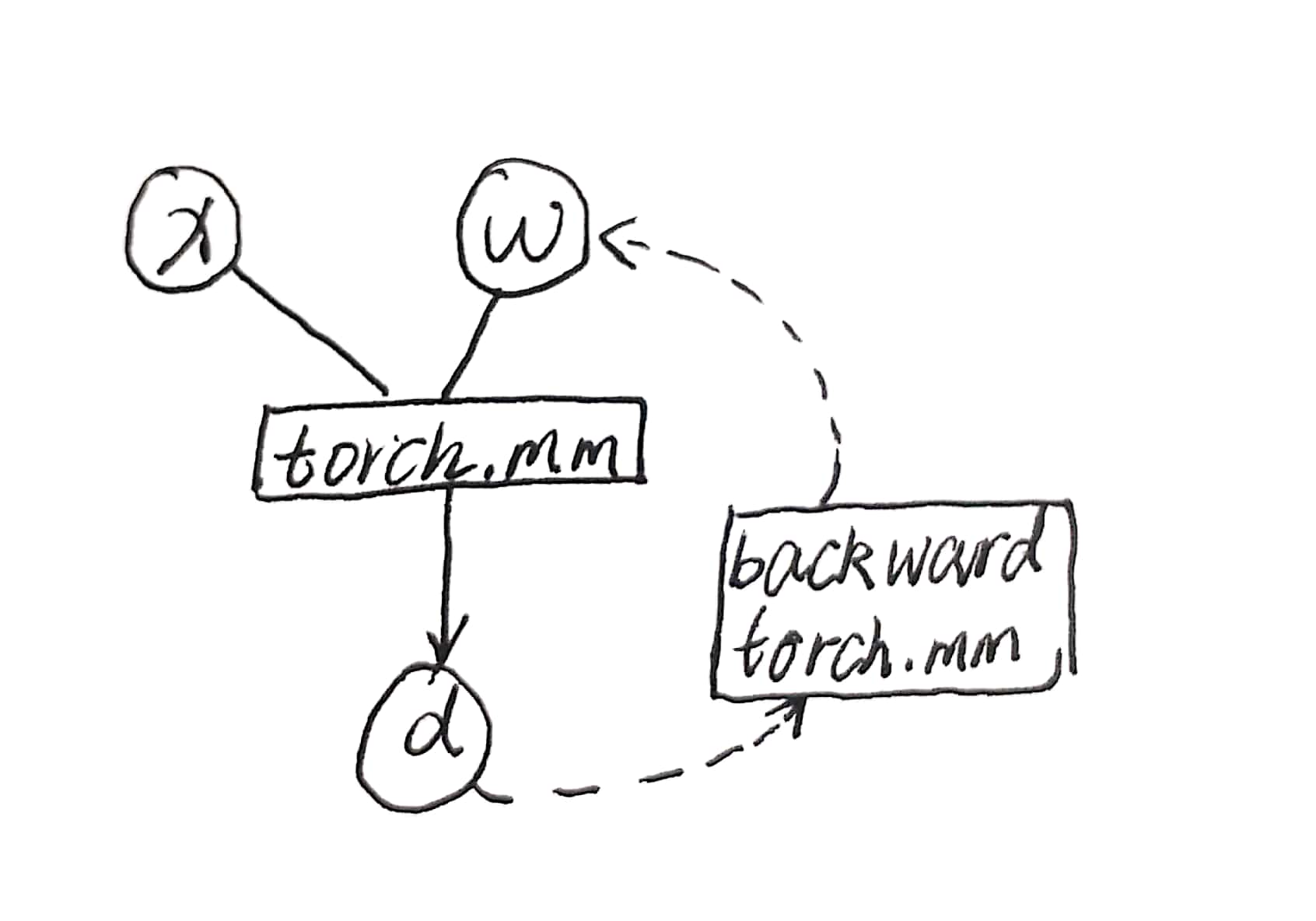
在计算得到d之后，反向求梯度的计算图就已经构建好了，而且w的梯度值的计算依赖于x的值，如果去掉代码中的注释，重新x -= 1的话，那么在反向传播的时候利用到x的值来求梯度就有误，为了防止这种错误发生，pytorch报错：

1
2
3

RuntimeError: one of the variables needed for gradient computation has been modified by an inplace operation: 
        [torch.FloatTensor [2, 3]] is at version 2; expected version 1 instead. 
        Hint: enable anomaly detection to find the operation that failed to compute its gradient, with torch.autograd.set_detect_anomaly(True).

造成错误的主要原因是，执行d=torch.mm(x, w)之后，反向求导机制保存了x的引用以便后续的反向求导计算。

x.data和x.detach()的区别

二者的相同之处在于：

都和x共享一块数据
都和x的计算历史无关
requires_grad=False

不同之处在于，x.data在某些情况下不安全，比如上述inplace operation 的第二种情况，将上述代码修改如下：

import torch

x = torch.randint(1, 5, (2, 3))
x = x.type_as(torch.FloatTensor(x.shape))
print(f'x = \n{x}\n')

w = torch.randint(1, 5, (3, 2))
w = w.type_as(torch.FloatTensor(w.shape))
w.requires_grad_(True)
print(f'w = \n{w}\n')

d = torch.mm(x, w)
x_ = x.data
x_ -= 1

d.sum().backward()
print(f'w.grad = \n{w.grad}')

输出结果如下：

x = 
tensor([[4., 2., 2.],
        [1., 1., 1.]])

w = 
tensor([[3., 2.],
        [2., 1.],
        [4., 2.]], requires_grad=True)

w.grad = 
tensor([[3., 3.],
        [1., 1.],
        [1., 1.]])

正确的w.grad应该是：

1
2
3

tensor([[5., 5.],
        [3., 3.],
        [3., 3.]])

发现运算真的将原来的x数值变化了然后再求导的（这里是将x矩阵中的所有元素都减一，可以手算一下结果是符合预期的）。

上述代码中，x_和x式共享一块数据空间的，改x_就相当于改x。release note 中指出, 如果想要 detach 的效果的话, 还是 detach() 安全一些.

import torch

x = torch.randint(1, 5, (2, 3))
x = x.type_as(torch.FloatTensor(x.shape))
print(f'x = \n{x}\n')

w = torch.randint(1, 5, (3, 2))
w = w.type_as(torch.FloatTensor(w.shape))
w.requires_grad_(True)
print(f'w = \n{w}\n')

d = torch.mm(x, w)
x_ = x.detach()
x_ -= 1

d.sum().backward()
print(f'w.grad = \n{w.grad}')

会有报错提示。

参考链接：

https://zhuanlan.zhihu.com/p/38475183

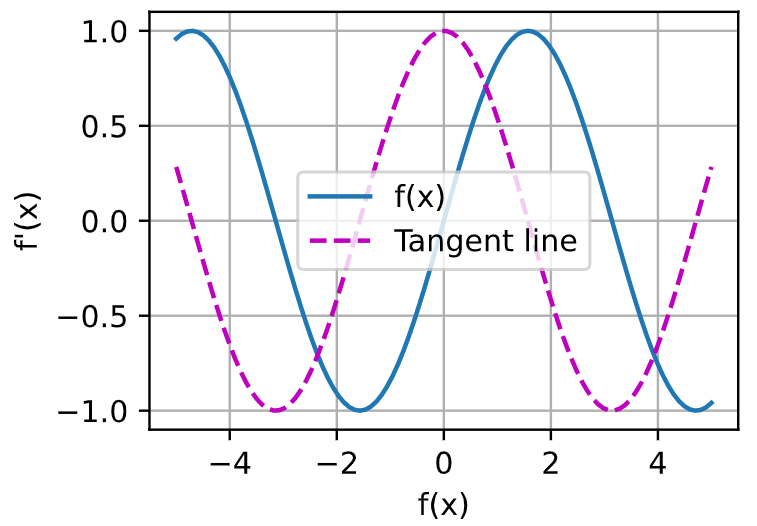
下面解决《动手学深度学习》的2.5章节的第五题：

代码如下：

x = torch.linspace(-5, 5, 100)
# 为x设置计算梯度
x.requires_grad_(True)
y = torch.sin(x)
# y反向传播,但是y是一个向量，所以需要传入参数
y.backward(torch.ones_like(x))
# 这里的y.detach和下一步的x.detach
# 是因为里面有步骤需要使用.numpy()的转换，有计算梯度的tensor不能使用.numpy()
y = y.detach()

from utils import d2l
d2l.plot(x.detach(), [y, x.grad], 'f(x)', "f'(x)", legend=['f(x)', 'Tangent line'])
d2l.plt.show()