基本概念

查找表：查找结构，用于查找的数据集合称为查找表，它由同一类型的数据元素（或记录）组成。

关键字：数据元素中唯一标识该元素的某个数据项的值，使用基于关键字的查找，查找结果应该是唯一的。

静态查找表：查找符合条件的数据元素（不会修改表中的数据）。

动态查找表：插入、删除某个数据元素。除了查找速度，也要关注插/删操作是否方便实现。

查找长度：在查找运算中，需要对比关键字的次数成为查找长度。

平均查找长度（ASL, Average Search Length)：所有查找过程中进行关键字的比较次数的平均值。

ASL=\sum_{i=1}^{n}P_iC_i

其中，n为数据元素的个数， $P_i$ 为查找第i个元素的概率， $C_i$ 为查找第i个元素的查找长度。

评价一个查找算法的效率的时候，通常考虑查找成功/查找失败两种情况的ASL。ASL的数量级反映了查找算法的时间复杂度。

顺序查找

思路是给定一个需要查找的元素x，遍历查找表直到找到为止。假设查找表的长度为n，那么对于其中的每一个元素i，计算平均查找长度为：

\mathbf{A S L}_{\text {成功 }}=\frac{1+2+3+\ldots+n}{n}=\frac{n+1}{2}

查找的时间复杂度为： $O(n)$ 。

查找失败的ASL为n+1。

查找表中的元素有序存放（递增/递减）eg:

7、13、19、29、37、43

查找目标：21

如果查找到29，发现29大于21但是仍未找到21，就可以断定查找失败。有序表的查找判定树如下（图来自王道考研）：

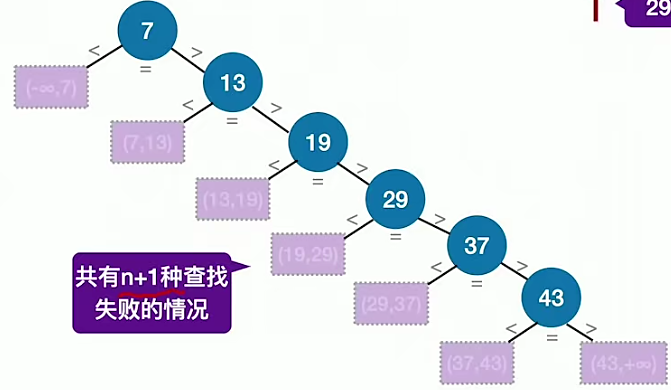
查找失败一共有n+1种情况，因为最后一个元素的两边的范围都是查找失败的范围。

我们认为查找失败的概率都是相等的，即给定一个元素，落在这n+1个范围内的概率是相等的，那么得到的查找失败的平均查找长度为：

\mathbf{A S L}_{\text {失败 }}=\frac{1+2+3+\ldots+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1}

注意，查找失败的分子上有两个n，分别表示的是元素43左右两个范围的查找次数。

如果被查找的数据不是等概率的，比如如下的序列：

7、13、19、29、37、43

其中被查找的概率依次为：

15%、5%、10%、40%、28%、2%

实际问题中，根据具体的需要来进行排列这些数据，如果按照概率大的元素排在前，那么最终成功的平均查找次数为：

ASL_{成功}=1^{\star} 0.4+2^{\star} 0.28+3^{\star} 0.15+4^{\star} 0.1+5^{\star} 0.05+6^{\star} 0.02=2.18

但是这样数据又变成了乱序，失败的平均查找次数和原来没有优化的一样，所以具体如何排列还需要考虑实际的应用。

分析折半查找的ASL需要画出查找判定树，比如给定有序序列：

7、10、13、16、19、29、32、33、37、41、43

画出查找判定树如下：

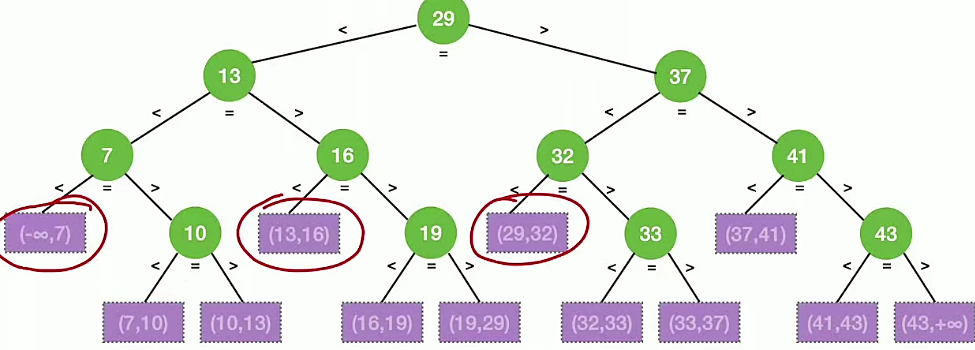
画出查找判定树然后分析查找成功和失败的ASL就容易了，对于成功ASL，每一层查找的次数为层的序数。那么容易计算：

\mathrm{ASL}_{\text {成功 }}=\left(1^{*} 1+2^{\star} 2+3^{\star} 4+4^{\star} 4\right) / 11=3

对于失败的ASL，我们认为任意一个元素x落在紫色范围内的概率相等，都为 $\frac{1}{12}$ ，对于第三层的数，需要查找3次，第4层的数需要查找4次，由此得到：

\text { ASL失败 }=\left(3^{*} 4+4^{\star} 8\right) / 12=11 / 3

折半查找的时间复杂度为 $O(log_2n)$

主要思想：将给定的看似无序的序列分为若干个子序列，称为“块”，块间有序，块内无序（这里的块间有序指的是每一个块中的最大值有序），然后使用一个索引表来存放序列的每一个块的最大值在原序列中的索引以及块的范围，比如下面这个示例（图来自王道考研系列课程）：

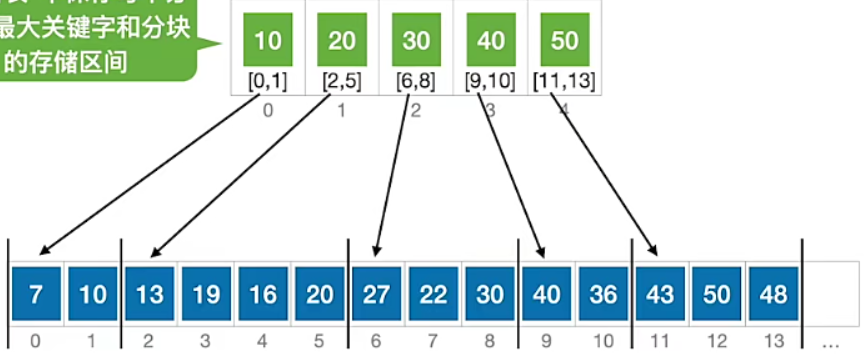
假设需要查找22，那么将22和每一个分块的最大值进行比较，如果小于某一个分块的最大值，说明该目标可能在该分块内，然后切换到该分块的起始位置进行查找，如果找到了则存在，否则不存在。这里判断目标在某一个块中，可以使用折半查找的方式而非遍历的方式来查找。

如果需要向满足分块查找要求的序列中插入一个元素，比如向上图中的序列插入元素8，为了维护表的特性，需要移动大量元素，为了解决这个问题，可以使用链式存储来解决，将上图中的表改成如下的链式存储：

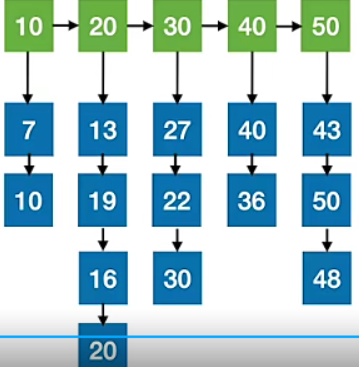
分块查找算法对于序列有比较特殊的要求，所以在实际应用中用的较少。