递归不需要我们去从最高层到最底层屡清楚,我们只需要考虑的是当前层与上一层之间的关系,将这种关系表示出来,然后将终止递归的条件确定清楚即可。至于一层一层往下调交给计算机来处理吧!试图想搞清楚计算机每一步都是怎么执行的,这样就很容易被绕进去。
现在很多 App 都有推荐注册返佣金的这个功能,用户 A 推荐用户 B 来注册,用户 B 又推荐了用户 C 来注册。我们可以说,用户 C 的“最终推荐人”为用户 A,用户 B 的“最终推荐人”也为用户 A,而用户 A 没有“最终推荐人”。一般来说,我们会通过数据库来记录这种推荐关系。在数据库表中,我们可以记录两列数据,其中 actor_id 表示用户 id,referrer_id 表示推荐人 id。那么,给定一个用户 ID,如何查找这个用户的“最终推荐人”?
可以使用如下的解决方案:
1 |
|
不过在实际项目中,上面的代码并不能工作:
第一,如果递归很深,可能会有堆栈溢出的问题。
第二,如果数据库里存在脏数据,我们还需要处理由此产生的无限递归问题。比如 demo 环境下数据库中,测试工程师为了方便测试,会人为地插入一些数据,就会出现脏数据。如果 A 的推荐人是 B,B 的推荐人是 C,C 的推荐人是 A,这样就会发生死循环。这个问题可以限制递归深度或者尾递归解决,不过还可以用一个更高级的解决方法:自动检测A-B-C-A这种“环”的存在。
递归注意点
递归代码要警惕堆栈溢出
在实际的软件开发中,编写递归代码时,我们会遇到很多问题,比如堆栈溢出。而堆栈溢出会造成系统性崩溃,后果会非常严重。
函数调用会使用栈来保存临时变量。每调用一个函数,都会将临时变量封装为栈帧压入内存栈,等函数执行完成返回时,才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大,调用层次很深,一直压入栈,就会有堆栈溢出的风险。
如何避免堆栈溢出呢?
-
可以通过在代码中限制递归调用的最大深度的方式来解决这个问题。递归调用超过一定深度(比如 1000)之后,我们就不继续往下再递归了,直接返回报错。如下伪代码所示:
1
2
3
4
5
6
7
8
9
10// 全局变量,表示递归的深度
int depth = 0;
int f(int n) {
++depth;
if (depth > 1000) throw exception;
if (n == 1) return 1;
return f(n - 1) + 1;
}但这种做法并不能完全解决问题,因为最大允许的递归深度跟当前线程剩余的栈空间大小有关,事先无法计算。如果实时计算,代码过于复杂,就会影响代码的可读性。所以,如果最大深度比较小,比如 10、50,就可以用这种方法,否则这种方法并不是很实用。
-
使用尾递归的方式。(参考:https://segmentfault.com/a/1190000022879214 )
在函数中return一个函数后,当前函数在栈内的调用记录会被删除,当前函数的执行上下文会从调用栈弹出。一般的递归在函数体中断点能够看到在栈内会创建大量的执行上下文并且不销毁(这就是造成栈溢出的原因);而尾递归是在栈内增加函数执行上下文,然后在该函数返回函数时,销毁当前函数执行上下文,创建返回的函数的执行上下文。所以尾递归中只有一个活跃的执行上下文。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20// 函数0是尾递归
function a(){
const r = c()
return r
}
// 函数1是尾递归
function a(){
return c()
}
// 函数2不是尾递归
function a(){
return c() * 20
}
// 函数3不是尾递归
function a(){
return c() || b()
}上面对于判断是否为尾递归都是自己在safari实际测试之后的结果。针对上面测试的结果总结一下:函数2不是尾递归,是因为c()调用后还需要进一步计算。函数3不是尾递归,是因为c()调用之后还有判断的动作以及可能的对于c的调用。而函数0和函数1是尾递归是因为返回的是一个函数或者一个已经计算好的值,而不需要再做多余的判断和计算。
下面使用尾递归来优化如下的累加项代码:
1
2
3
4int fn(n){
if(n <= 1) return 1;
return n + fn(n-1);
}尾递归代码(针对数组里面所有项的累加递归):
1
2
3
4
5int fn(arr, sum = 0){
if(arr.length === 0) return sum;
return fn(arr.slice(1), arr[0] + sum);
}
fn([1,2,3,4])尾递归也有自己的一些缺陷。如尾递归是一个隐式行为,如果代码存在死循环尾递归调用,爆栈后难以被开发者察觉;堆栈信息会丢失,造成调试困难。还有目前各大浏览器厂商对尾递归的支持和兼容性不太好。所以在尾递归目前还不被各大浏览器支持的情况下,可以对递归的一些重复内容做优化。
递归代码要警惕重复计算
使用递归算法实现斐波那契数列代码如下:
1 | int fib(int N) { |
将n=20的递归树画出来,如下图所示(图取自https://labuladong.github.io/algo/3/23/57/):
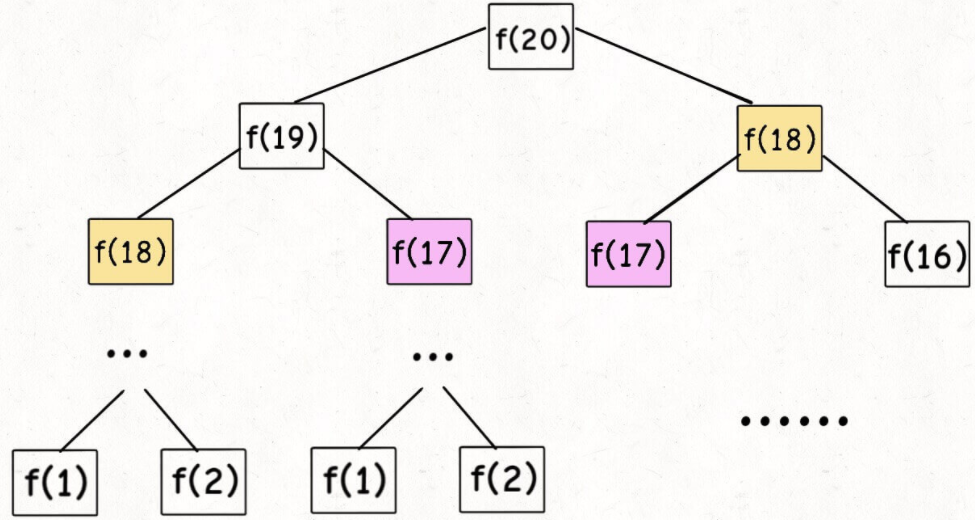
比如计算就需要计算和,而计算需要计算和,这里的被重复计算了多次,这就是重复计算的问题。
为了避免重复计算,可以通过一个数据结构来保存已经求解的。当递归调用的时候,先看下是否已经求解过。如果是,则直接从散列表中取值返回,不需要重复计算。
参考:
https://labuladong.github.io/algo/3/23/57/
在时间效率上,递归代码里多了很多函数调用,当这些函数调用的数量较大时,就会积聚成一个可观的时间成本。在空间复杂度上,因为递归调用一次就会在内存栈中保存一次现场数据,所以在分析递归代码空间复杂度时,需要额外考虑这部分的开销
将递归代码改为非递归代码
递归有利有弊,利是递归便于理解,写起来简洁;弊是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多时间等。所以在开发过程中,我们要根据实际情况来确定是否用递归的方式来实现。
因为递归本身就是借助栈来实现的,只不过我们使用的栈是系统或者虚拟机本身提供的,我们没有感知罢了。如果我们自己在内存堆上实现栈,手动模拟入栈、出栈过程,这样任何递归代码都可以改写成看上去不是递归代码的样子。
数据规模较大的情况最好使用非递归来实现。
思考
我们平时调试代码喜欢使用 IDE 的单步跟踪功能,像规模比较大、递归层次很深的递归代码,几乎无法使用这种调试方式。对于递归代码,有什么好的调试方法呢?
1.打印日志发现,递归值。
2.结合条件断点进行调试。

